MULTIPLE AUTOSOMAL COMBINATIONS



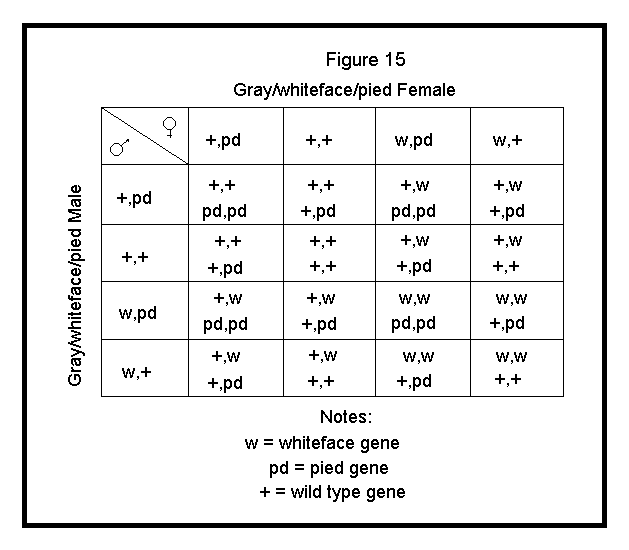
In the example below, I will show and discuss two autosomal traits, each specified by a different pair of independently assorting autosomal genes, that is, genes on different (nonhomologous) chromosomes. Once again, I will present the worst case scenario (i.e., a cross involving the most calculations), a dihybrid cross. A dihybrid cross is a cross involving parents that are both heterozygous for two traits.

For this example, I will cross a Gray Male heterozygous for Whiteface (+,w) and Pied (+,pd) to a Gray Female heterozygous for Whiteface (+,w) and Pied (+,pd). The gametes that each parent will produce are as follows:


+, pd
+, +
w, pd
w, +


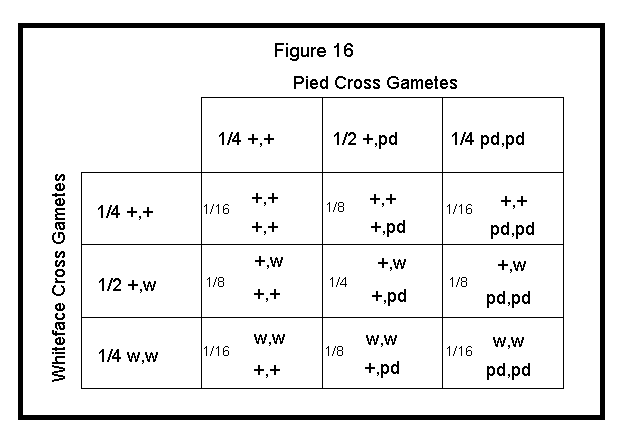
These gametes are applied to the Punnett square as shown in Figure 15.




Summary of the outcome from this cross is as follows:


GenotypePhenotype
1/16 (+,+)(+,+)
1/8 (+,+)(+,pd)
1/4 (+,w)(+pd)
1/8 (+,w)(+,+)

9/16 Gray
1/16 (+,+)(pd,pd)
1/8 (+,w)(pd,pd)


3/16 Gray Pied
1/8 (w,w)(+,pd)
1/16 (w,w)(+,+)


3/16 Whiteface
1/16 (w,w)(pd,pd)––––––>1/16 Whiteface Pied

As you can see, the phenotypic ratio for a dihybrid cross is 9:3:3:1. For a trihybrid cross in which both parents are heterozygous for three independently assorting autosomal traits the phenotypic ratio is 27:9:9:9:3:3:3:1. In further genetics study, you will come across these and other ratios for various types of crosses.

A simpler method for calculating the expected outcome for a cross involving two different autosomal genes is as follows:

First, do a cross for the whiteface mutation

+,w crossed to +,w


This will produce

1/4 +,+
1/2 +,w
1/4 w,w


Second, do a cross for the pied mutation

+,pd crossed to +,pd


This will produce

1/4 +,+
1/2 +,pd
1/4 pd,pd


Third, apply the product of the first cross to the left side of the Punnett square and the product of the second cross to the top of the Punnett square.


Finally, work out each block of the Punnett square by multiplying the respective fractions and combining alleles. See Figure 16 below.




Applying the above approach to three or more different traits would be quite difficult. For more than two autosomal traits, I would apply the Branching system method for determining the statistical probability of offspring. The below example shows a trihybrid cross. This cross is a worst case scenario (i.e., requires the most calculations). Both parents are heterozygous for whiteface, pied and fallow. Again, I solved each cross separately to derive the following:


+,w crossed to +, w ----------> 1/4 +,+ ; 1/2 +,w ; 1/4 w,w

+,pd crossed to +,pd ----------> 1/4 +,+ ; 1/2 +,pd ; 1/4 pd,pd

+,f crossed to +,f --------------> 1/4 +,+ ; 1/2 +,f ; 1/4 f,f

This outcome is then applied to the Branching System method as shown in Figure 17.




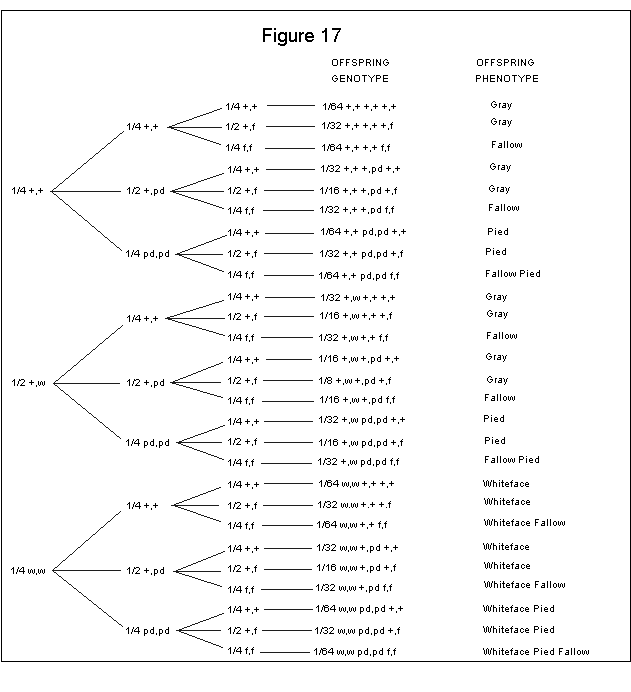
If you add up the phenotypes of Figure 17, you will come out with the following:


27/64 Gray
9/64 Fallow
9/64 Pied
9/64 Whiteface
3/64 Fallow Pied
3/64 Whiteface Fallow
3/64 Whiteface Pied
1/64 Whiteface Pied Fallow


Let us now add some sex-linked genes to the above cross. If the male was heterozygous for the Lutino mutation (Xl,+,X+,+) and the female is a hemizygous Pearl (X+,pl,Y) then by just solving for a cross involving these sex-linked traits you derive the following:



1/4 Xl,+, X+pl–––Gray Male
heterozygous for
lutino and pearl
1/4 X+,+, X+pl–––Gray Male
heterozygous
for pearl
1/4 X+,+, Y –––Gray Female
1/4 Xl,+, Y –––Lutino Female


Each of these four outcomes would then be applied separately to the above autosomal outcome of Figure 17. There are 27 autosomal genotypes listed in Figure 17. After applying the four sex linked outcomes, there would be 108 different genotypes.

Keep in mind that if the male is heterozygous for two or more sex linked traits then you must also factor in crossover and their particular rate of occurrence. Crossover is discussed in the next section.